
인트로
다익스트라 알고리즘은 그래프의 탐색 알고리즘으로
BFS가 가중치 없는 그래프의 최단경로를 찾는 알고리즘이라면
다익스트라 알고리즘은 가중치가 있는 그래프의 최단경로를 구할 때 사용된다.
참고로 다익스트라 길 찾기 알고리즘은 DFS, BFS와 마찬가지로 완전 탐색 알고리즘에 속한다.
다익스트라(Dijkstra) 이해하기
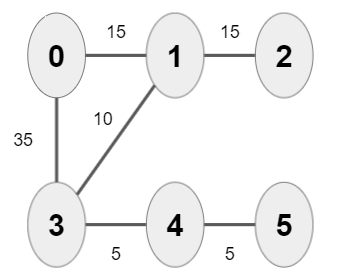
1) 아래와 같은 가중치 그래프가 있다. 0번 정점에서 시작해 5번 정점까지의 최단거리를 구해보자.
최단거리를 저장할 배열(DIST)이 다음과 같은 형태로 있다. DIST[ ∞, ∞, ∞, ∞, ∞, ∞ ] (+ 아직 최단거리를 모르니 모두 ∞로 초기화한다.)
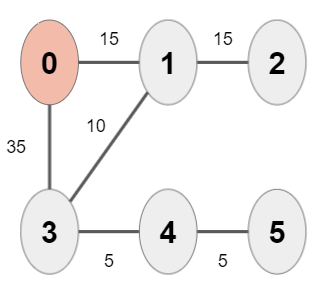
2) 시작 정점인 "0"번 정점을 방문한다.
시작 정점인 "0"번 정점은 최단거리가 "0"이므로 DIST[ 0, ∞, ∞, ∞, ∞, ∞ ]를 갱신하고 "0"번 정점과 인접한 정점까지의 최단거리를 계산한다. DIST[0,15, ∞, 35, ∞, ∞ ]
3) DIST[0,15, ∞, 35, ∞, ∞ ]를 기준으로 방문한 적이 없으며 거리가 가장 짧은 정점("1"번)을 방문한다.
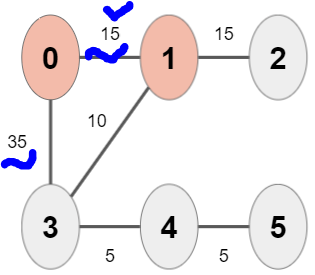
4) "0"번 정점에서 그랬듯 "1"번 정점과 인접하며 방문하지 않은 정점인 "2"번과 "3"번 정점의 최단 거리를 계산한다.
다익스트라의 핵심은 "3"번 정점의 최단거리가 갱신됐다는 것이다. "0" -> "3"의 비용인 35보다 "0" -> "1" -> "3"의 비용인 25(15 + 10)가 더 짧으니 최단거리를 갱신한다. [ 0, 15, 30, 25, ∞, ∞ ]

다익스트라(Dijkstra) : C# 코드
class Program
{
static void Main(string[] args)
{
GraphArray g = new GraphArray(6);
g.AddEdge(0, 1, 15);
g.AddEdge(0, 3, 35);
g.AddEdge(1, 2, 15);
g.AddEdge(1, 3, 10);
g.AddEdge(3, 4, 5);
g.AddEdge(4, 5, 5);
g.Dijkstra(0, 5);
}
}class GraphArray
{
private int[,] _adj;
private int _size;
List<int> _path = new List<int>();
public GraphArray(int n)
{
_size = n;
_adj = new int[_size, _size];
}
public void AddEdge(int a, int b, int cost = 1)
{
_adj[a, b] = cost;
_adj[b, a] = cost;
}
public void Dijkstra(int start, int dest)
{
bool[] visited = new bool[_size];
int[] distance = new int[_size];
int[] parent = new int[_size];
Array.Fill(distance, Int32.MaxValue);
distance[start] = 0;
parent[start] = start;
while (true)
{
//인접하면서 제일 가까운 후보를 찾기
int now = -1;
int closest = Int32.MaxValue;
for (int i = 0; i < _size; i++)
{
//이미 방문했으면 스킵
if (visited[i])
continue;
//시작점으로 부터 발견된 적 없는 경우
if (distance[i] == Int32.MaxValue)
continue;
//가장 가까운 후보를 기억하기
if (distance[i] < closest)
{
closest = distance[i];
now = i;
}
}
if (now == -1)
break;
visited[now] = true;
//방문한 정점과 인접한 정점중
//최단 거리를 계산해서 갱신한다.
for (int next = 0; next < _size; next++)
{
if (_adj[now, next] == 0)
continue;
if (visited[next])
continue;
int nextDist = distance[now] + _adj[now, next];
//최단거리 갱신
if (nextDist < distance[next])
{
distance[next] = nextDist;
parent[next] = now;
}
}
}
CalcPathFromParent(parent, dest);
}
void CalcPathFromParent(int[] parent, int dest)
{
Console.WriteLine($"{dest}까지 최단 경로");
while (parent[dest] != dest)
{
_path.Add(dest);
dest = parent[dest];
}
_path.Add(dest);
_path.Reverse();
foreach (int n in _path)
Console.WriteLine(n);
}
}
'Algorithm > 탐색' 카테고리의 다른 글
| [Algorithm] 이진 탐색 (이분 탐색, Binary Search) 코드와 시간 복잡도 (0) | 2021.09.16 |
|---|---|
| [Algorithm] A* 알고리즘 : 최단 경로 탐색 (4) | 2021.09.03 |
| [Algorithm] 이진 탐색 트리 (Binary Search Tree, BST) + 전위 중위 후위 순회 (1) | 2021.08.27 |
| [Algorithm] BFS (Breadth First Search, 너비 우선 탐색) 알고리즘 (0) | 2021.08.23 |
| [Algorithm] DFS (Depth First Search, 깊이 우선 탐색) 알고리즘 (1) | 2021.08.17 |

