인트로
그래프의 탐색 알고리즘인 BFS(Breadth First Search, 너비 우선 탐색)를 구현해보려 한다.
DFS와 다르게 BFS는 주로 한 가지 목적으로 사용된다.
그것은 가중치가 없는 그래프의 최단 경로를 구할 때 사용된다.
본 포스팅에선 C# 기반 배열과 리스트(List)로 BFS를 구현하는 간단한 코드와 최단 경로 출력 코드를 소개하려 한다.
결론부터 말하면 Queue를 사용해서 BFS를 구현했다.
DFS가 궁금하다면?
DFS (Depth First Search, 깊이 우선 탐색) 알고리즘
[Algorithm] DFS (Depth First Search, 깊이 우선 탐색) 알고리즘
인트로 그래프의 탐색 알고리즘인 DFS(Depth First Search, 깊이 우선 탐색)를 구현해보려 한다. 그래프라는 건 추상적인 개념이다. 0번 정점과 1번 정점이 연결되어 있다는 정보만 있을 뿐 실질적으로
kangworld.tistory.com
BFS 이해하기
1) Queue는 비어있고 아래와 같은 그래프가 있다.

2) BFS를 "0"번 정점부터 시작한다고 가정해보자. "0"번 정점을 방문하고 Queue에 "0"을 삽입한다.
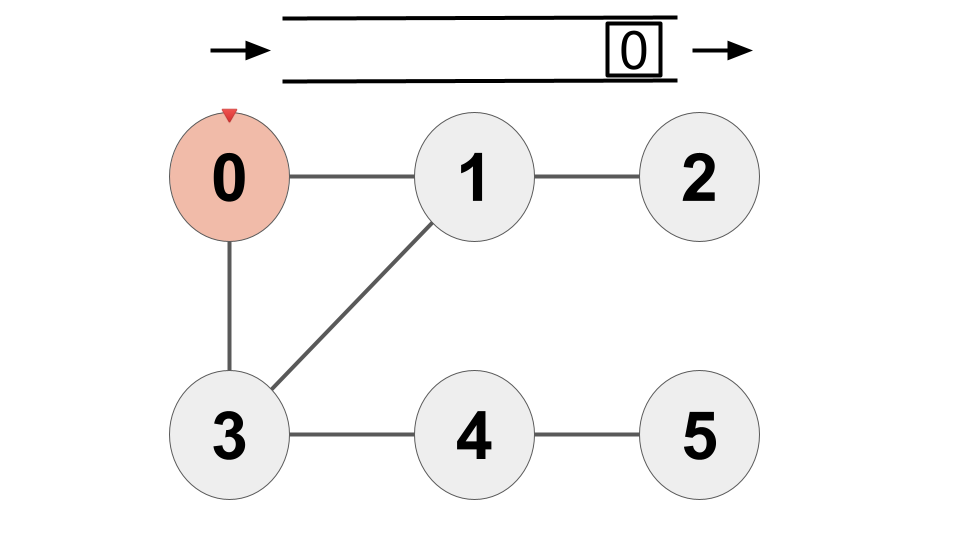
3) Queue에서 "0"을 빼내고 "0"과 인접한 "1"과 "3"을 Queue에 삽입한다.

4) Queue에서 "1"을 빼내고 "1"과 인접한 "2"를 Queue에 삽입한다.

5) Queue에서 "3"을 빼내고 "3"과 인접한 "4"를 Queue에 삽입한다.

6) Queue에서 "2"을 빼낸다. "2"와 인접한 정점이 없으므로 Queue에 아무것도 Push하지 않는다.

7) Queue에서 "4"을 빼내고 "4"과 인접한 "5"를 Queue에 삽입한다.
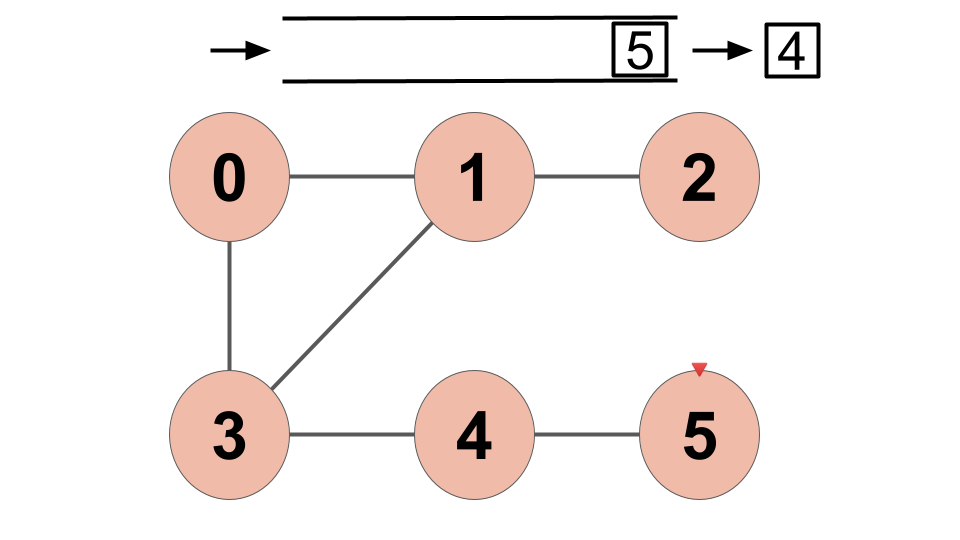
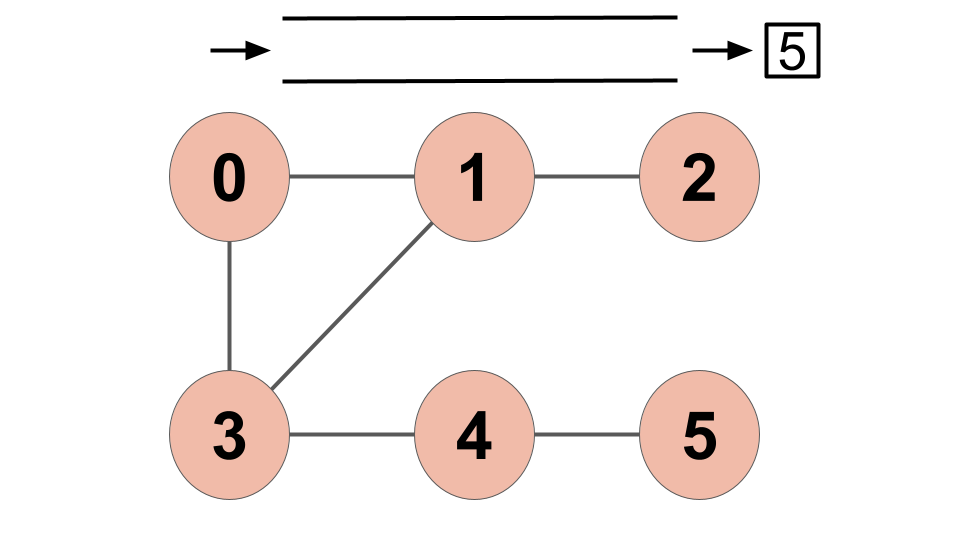
8) Queue에서 "5"을 빼낸다. "5"와 인접한 정점이 없으므로 Queue에 아무것도 Push하지 않는다.
Queue에 아무것도 들어있지 않아 BFS는 종료된다.
BFS 코드 : 배열
using System;
using System.Collections.Generic;
namespace BFS
{
class GraphArray
{
private int[,] _adj;
private int _size;
public GraphArray(int n)
{
_size = n;
_adj = new int[_size, _size];
}
public void AddEdge(int a, int b)
{
_adj[a, b] = 1;
_adj[b, a] = 1;
}
// 1) now를 방문
// 2) now와 연결된 정점을 확인해서 "방문안했다면" 방문하기
public void BFS(int start)
{
Queue<int> q = new Queue<int>();
bool[] visited = new bool[_size];
q.Enqueue(start);
visited[start] = true;
while (q.Count > 0)
{
int now = q.Dequeue();
Console.WriteLine(now);
for (int next = 0; next < _size; next++)
{
//연결되었는가?
if (_adj[now, next] == 0)
continue;
//이미 방문했는가?
if (visited[next] == true)
continue;
q.Enqueue(next);
visited[next] = true;
}
}
}
}
class Program
{
static void Main(string[] args)
{
GraphArray g = new GraphArray(6);
g.AddEdge(0, 1);
g.AddEdge(0, 3);
g.AddEdge(1, 2);
g.AddEdge(1, 3);
g.AddEdge(3, 4);
g.AddEdge(4, 5);
g.BFS(0);
}
}
}
BFS 코드 : 리스트(List)
using System;
using System.Collections.Generic;
namespace BFS
{
class GraphList
{
private List<int>[] _adj;
private int _size;
public GraphList(int n)
{
_size = n;
_adj = new List<int>[_size];
for (int i = 0; i < _size; i++)
_adj[i] = new List<int>();
}
public void AddEdge(int a, int b)
{
_adj[a].Add(b);
_adj[b].Add(a);
}
// 1) now를 방문
// 2) now와 연결된 정점을 확인해서 "방문안했다면" 방문하기
public void BFS(int start)
{
Queue<int> q = new Queue<int>();
bool[] visited = new bool[_size];
q.Enqueue(start);
visited[start] = true;
while (q.Count > 0)
{
int now = q.Dequeue();
Console.WriteLine(now);
foreach (int next in _adj[now])
{
// 이미 방문했는가?
if (visited[next])
continue;
q.Enqueue(next);
visited[next] = true;
}
}
}
}
class Program
{
static void Main(string[] args)
{
GraphList g = new GraphList(6);
g.AddEdge(0, 1);
g.AddEdge(0, 3);
g.AddEdge(1, 2);
g.AddEdge(1, 3);
g.AddEdge(3, 4);
g.AddEdge(4, 5);
g.BFS(0);
}
}
}출력이 잘 된다.

BFS : 최단경로 출력
GraphArray의 BFS 메서드를 수정해서 A노드에서 B노드까지 길이(노드와 노드 사이의 길이는 모두 1)와 최단 경로를 출력하도록 코드를 수정했다. (+ 코드가 깔끔하지 못하네요.. 이해 부탁드립니다.)
참고로 아래의 주요 변수들이 추가되었다.
경로 출력은 어렵지 않으니 코드를 보고 이해하길 바란다.
List<int> path = new List<int>();int[] parent = new int[_size];
/*
자신의 부모 노드의 번호를 저장하는 배열
ex) parent[1] == 0
ex) parent[3] == 0
ex) parent[2] == 1
*/int[] distance = new int[_size];
/*
시작점으로부터 거리를 저장하는 배열
*/List<int> _path = new List<int>();
// 1) now를 방문
// 2) now와 연결된 정점을 확인해서 "방문안했다면" 방문하기
public void BFS(int start, int dest)
{
Queue<int> q = new Queue<int>();
bool[] visited = new bool[_size];
int[] parent = new int[_size];
int[] distance = new int[_size];
q.Enqueue(start);
visited[start] = true;
parent[start] = start;
distance[start] = 0;
while(q.Count > 0)
{
int now = q.Dequeue();
for(int next = 0; next < _size; next++)
{
//연결되었는가?
if (_adj[now, next] == 0)
continue;
//이미 방문했는가?
if (visited[next] == true)
continue;
q.Enqueue(next);
visited[next] = true;
parent[next] = now;
distance[next] = distance[now] + 1;
}
}
CalcPathFromParent(parent, dest);
}
void CalcPathFromParent(int[] parent, int dest)
{
Console.WriteLine($"{dest}까지 최단 경로");
while (parent[dest] != dest)
{
_path.Add(dest);
dest = parent[dest];
}
_path.Add(dest);
_path.Reverse();
foreach (int n in _path)
Console.WriteLine(n);
}
'Algorithm > 탐색' 카테고리의 다른 글
| [Algorithm] 이진 탐색 (이분 탐색, Binary Search) 코드와 시간 복잡도 (0) | 2021.09.16 |
|---|---|
| [Algorithm] A* 알고리즘 : 최단 경로 탐색 (4) | 2021.09.03 |
| [Algorithm] 다익스트라 알고리즘 : 최단 경로 탐색(1) - 배열 (0) | 2021.08.31 |
| [Algorithm] 이진 탐색 트리 (Binary Search Tree, BST) + 전위 중위 후위 순회 (1) | 2021.08.27 |
| [Algorithm] DFS (Depth First Search, 깊이 우선 탐색) 알고리즘 (1) | 2021.08.17 |

