인트로
그래프의 탐색 방법으로 DFS와 BFS가 대표적이다.
트리는 특정 조건을 만족하는 그래프이다. 따라서 트리에 BFS와 DFS 탐색 알고리즘을 적용할 수 있다.
본 포스팅에선 DFS에 기반한 이진 트리 탐색 알고리즘인 전위 순회(Preorder Traversal), 중위 순회(Inorder Traversal), 후위 순회(Postorder Traversal)를 다루려 한다.
(+ 2021.09.01 추가
이진 트리의 순회 알고리즘을 소개하며 이진 트리와 이진 탐색 트리를 모두 소개하다 보니 전달하려는 의미가 모호해졌네요.일반적으로 이진 트리의 순회는 전위 중위 후위 순회가 있습니다. 물론 이진 탐색 트리도 일종의 이진 트리이기에 순회 가능합니다. 나아가 이진 탐색 트리는 "이진 탐색"에 기반한 추상 자료형이기에 특정 데이터를 아주 빠른 시간(O(logN)에 찾을 수 있습니다. 본 포스팅에선 이진 탐색 트리보단 이진 트리 순회에 초점을 두고 작성했음을 염두에 두시면 될 것 같습니다.
시간이 되면 이진 트리와 이진 탐색 트리를 분리해서 다시 글을 작성하도록 하겠습니다. )
이진 트리(Binary Tree)
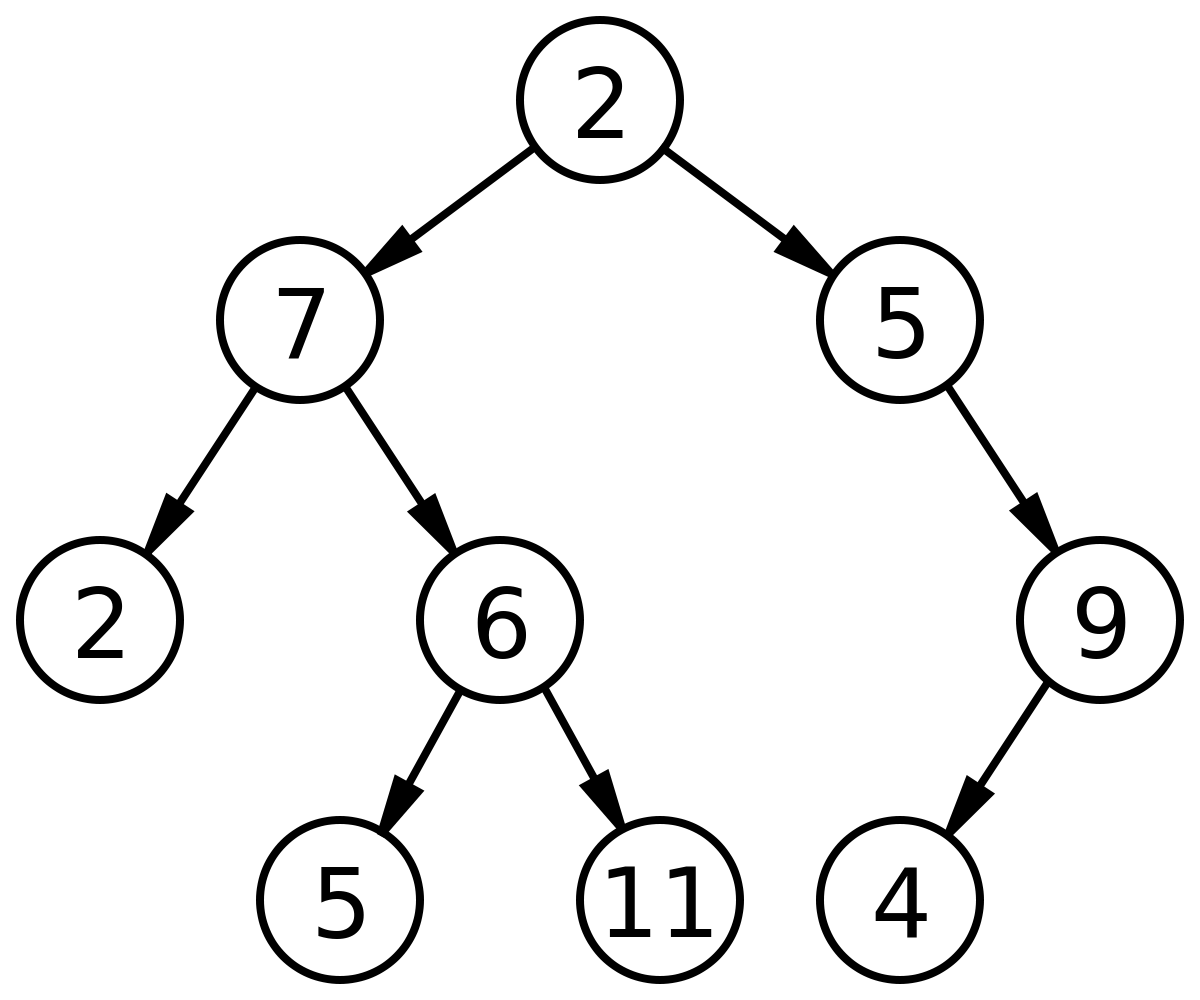
트리의 부모 노드가 최대 두 개의 자식 노드만을 가질 때 해당 트리를 "이진트리"라고 부르며
DFS기반 탐색 알고리즘인 전위 순회(Preorder Traversal), 중위 순회(Inorder Traversal), 후위 순회(Postorder Traversal)를 적용하여 이진트리 전체 노드를 탐색할 수 있다.
이진 탐색 트리(Binary Search Tree)
이진 탐색 트리는 특정 조건을 만족하는 이진트리이다.
[※ 이진 탐색 트리 조건 ※]
1) 부모 노드의 왼쪽 노드는 부모 노드보다 작아야 한다.
2) 부모 노드의 오른쪽 노드는 부모 노드보다 커야 한다.
이진 탐색 트리는 말 그대로 이진 탐색에 트리의 개념이 더해진 것으로 특정 값을 탐색하는 것에 빠른 성능을 보여준다.
[ 평균적으로 O(NlogN), 최악의 경우 O(N) ]
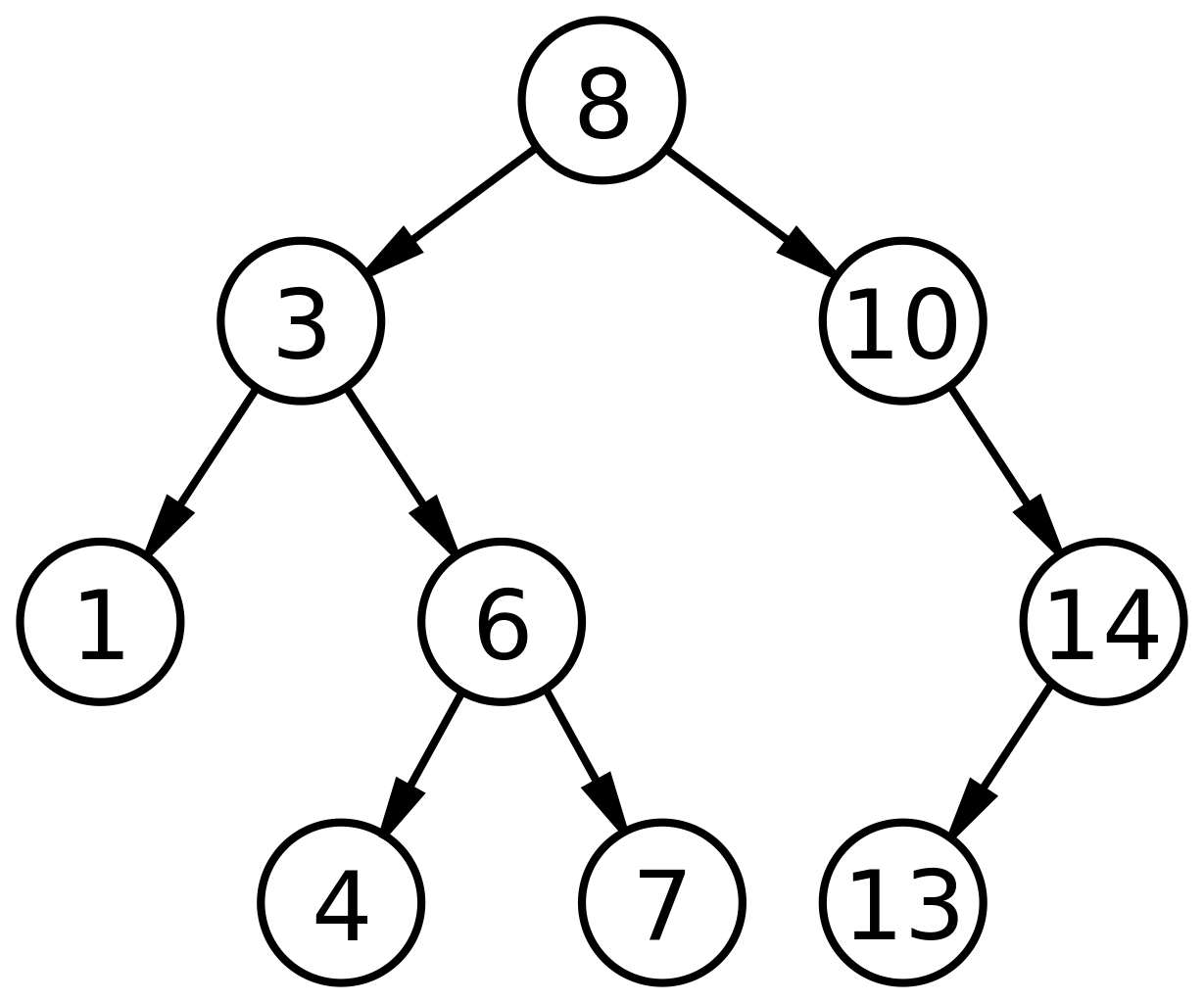
예를 들어 아래의 그림에서 "7"을 찾고 싶다면 Root(8)부터 탐색이 시작된다.
1) "7"이 Root(8) 보다 큰가 작은가? : 작음 (작다면 왼쪽 크다면 오른쪽 노드로 옮겨간다, 왼쪽 노드(3)로 이동)
2) "7"이 Node(3) 보다 큰가 작은가? : 큼 (오른쪽 노드(6)로 이동)
3) "7"이 Node(6) 보다 큰가? 작은가? : 큼 (오른쪽 노드(7)로 이동)
4) "7"과 Node(7)의 값이 동일하다 : 탐색 종료
순회 : 전위(Preorder) 중위(Inorder) 후위(Postorder)
(※참고※ 이진 탐색 트리에서 순회를 진행합니다.)

1) 전위 순회(Preorder Traversal)
① 현재 노드를 출력(처리)한다.
② 왼쪽 노드를 방문
③ 오른쪽 노드를 방문
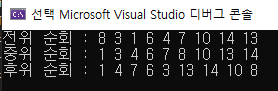
8 - 3 - 1 - 6 - 4 - 7 - 10 - 14 - 13
2) 중위 순회(Inorder Traversal)
① 왼쪽 노드를 방문
② 현재 노드를 출력(처리)한다.
③ 오른쪽 노드를 방문
1 - 3 - 4 - 6 - 7 - 8 - 10 - 13 - 14
(이진 탐색 트리에서 중위 순회는 정렬된 형태로 출력된다.)
3) 후위 순회(Postorder Traversal)
① 왼쪽 노드를 방문
② 오른쪽 노드를 방문
③ 현재 노드를 출력(처리)한다.
1 - 4 - 7 - 6 - 3 - 13 - 14 - 10 - 8
이진 탐색 트리 순회 코드 ( C++ BASE )
Node Class
#include <iostream>
using namespace std;
template <class T>
class Node
{
public:
T data;
Node* LeftNode;
Node* RightNode;
Node(T value)
{
this->data = value;
this->LeftNode = NULL;
this->RightNode = NULL;
}
};BinarySearchTree Class
template <class T>
class BinarySearchTree
{
public:
Node<T>* Root;
bool Add(T value)
{
Node<T>* before = NULL;
Node<T>* after = this->Root;
while (after != NULL)
{
before = after;
if (value < after->data)
after = after->LeftNode;
else if (value > after->data)
after = after->RightNode;
else return false;
}
Node<T>* newNode = new Node<T>(value);
if (this->Root == NULL)
Root = newNode;
else if (value < before->data)
before->LeftNode = newNode;
else before->RightNode = newNode;
return true;
}
Node<T> Find(T value)
{
Find(value, this->Root);
}
void PreOrder(Node<T>* node)
{
if (node != NULL)
{
cout << node->data << " ";
PreOrder(node->LeftNode);
PreOrder(node->RightNode);
}
}
void InOrder(Node<T>* node)
{
if (node != NULL)
{
InOrder(node->LeftNode);
cout << node->data << " ";
InOrder(node->RightNode);
}
}
void PostOrder(Node<T>* node)
{
if (node != NULL)
{
PostOrder(node->LeftNode);
PostOrder(node->RightNode);
cout << node->data << " ";
}
}
private:
Node<T> Find(T value, Node<T>* node)
{
while (node != NULL)
{
if (node.data == value) return node;
else if (node.data < value)
return Find(value, node->LeftNode);
else return Find(value, node->RightNode);
}
return NULL;
}
};Main Code
int main(void) {
BinarySearchTree<int>* BST = new BinarySearchTree<int>();
BST->Add(8);
BST->Add(3);
BST->Add(10);
BST->Add(1);
BST->Add(6);
BST->Add(4);
BST->Add(7);
BST->Add(14);
BST->Add(13);
cout << "전위 순회 : ";
BST->PreOrder(BST->Root);
cout << endl; cout << "중위 순회 : ";
BST->InOrder(BST->Root);
cout << endl; cout << "후위 순회 : ";
BST->PostOrder(BST->Root); cout << endl;
}
'Algorithm > 탐색' 카테고리의 다른 글
| [Algorithm] 이진 탐색 (이분 탐색, Binary Search) 코드와 시간 복잡도 (0) | 2021.09.16 |
|---|---|
| [Algorithm] A* 알고리즘 : 최단 경로 탐색 (4) | 2021.09.03 |
| [Algorithm] 다익스트라 알고리즘 : 최단 경로 탐색(1) - 배열 (0) | 2021.08.31 |
| [Algorithm] BFS (Breadth First Search, 너비 우선 탐색) 알고리즘 (0) | 2021.08.23 |
| [Algorithm] DFS (Depth First Search, 깊이 우선 탐색) 알고리즘 (1) | 2021.08.17 |

