[Algorithm] 삽입 정렬(Insertion Sort) 코드와 시간 복잡도 (+ 예제)

인트로

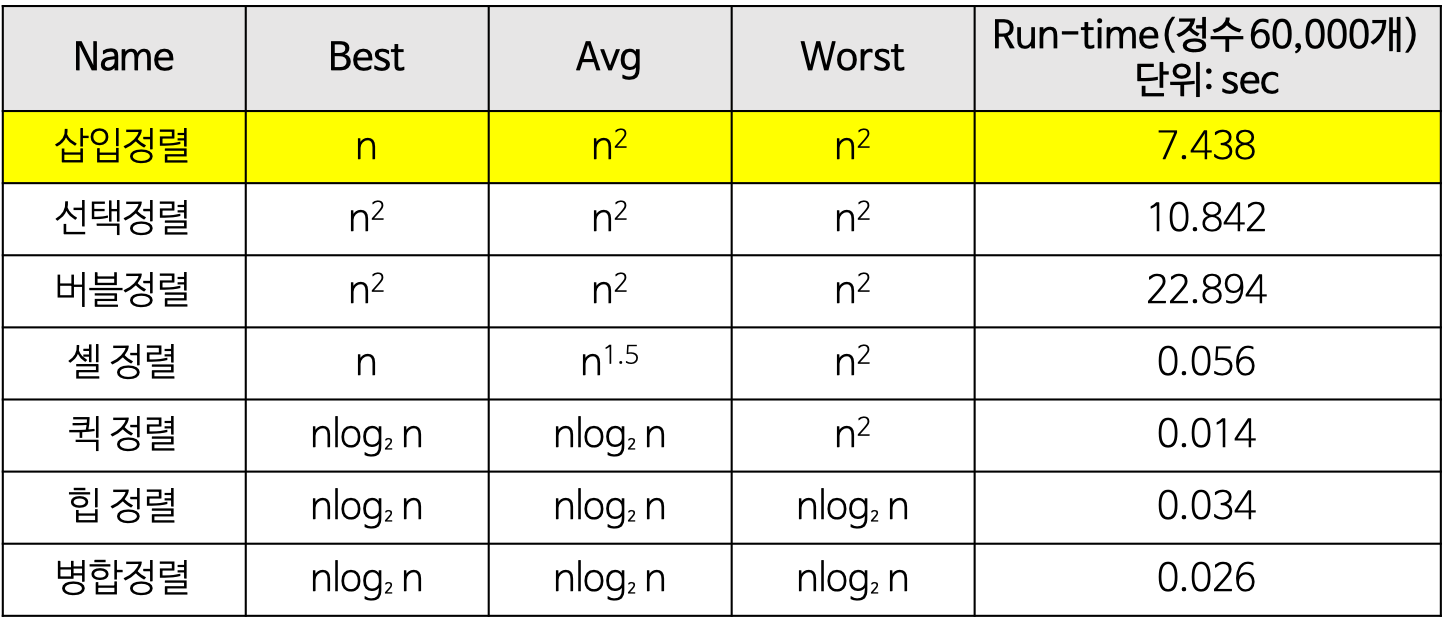
기초 정렬 알고리즘 마지막 파트인 삽입 정렬(Insertion Sort)을 알아보자.

 

재밌게도 삽입 정렬은 데이터의 배치에 따라 O(N) 시간 복잡도를 가진다.

개인적인 생각으로 버블 정렬의 한 단계 진화한 모습이 삽입 정렬이 아닐까 한다.

 

삽입 정렬과 관련된 문제는 해당 포스팅을 참고하세요 :)

[Algorithm] level0 : LRU(Least Recently Used)

[Algorithm] level0 : LRU(Least Recently Used)

 

삽입 정렬(Insertion Sort) : 개념

삽입 정렬은 "정렬되지 않은 데이터"를 "정렬된 데이터들 사이에 끼워 넣는" 정렬이다.

 

https://jinhyy.tistory.com/9

지금부터 삽입 정렬의 중간 과정을 설명하려 한다. 

 

붉은색 : 정렬되지 않은 곳

파란색 : 정렬된 곳

[1] [4] [5] [3] [9]

[1] [4] [5] 까지는 정렬된 상태이고 [3]과 [9]를 정렬된 데이터 사이에 끼워 넣어야 한다.

 

(※참고※ 삽입 정렬은 "0"번 원소는 이미 정렬되었다고 가정하고 "1"번 원소부터 정렬을 시작한다.)

 

[ Cycle 1 ]

시작

▶ [1] [4] [5] [3] [9]

 

[3]이 [5]보다 작으니 [5]를 한 칸 뒤로 밀어버린다. 

▶ [1] [4] [ ] [5] [9]

 

[3]이 [4]보다 작으니 [4]를 한 칸 뒤로 밀어버린다. 

▶ [1] [ ] [4] [5] [9]

 

[3]이 [1]보다 크니 [1] 뒤에 [3]을 삽입한다. 

▶ [1] [3] [4] [5] [9]

 

[ Cycle 2 ]

시작

▶ [1] [3] [4] [5] [9]

 

[9]가 [5]보다 크니 [9]자리에 다시 [9]를 삽입한다. 

▶ [1] [3] [4] [5] [9]

 

삽입 정렬(Insertion Sort) : 코드

#include <iostream>
#include <vector>

using namespace std;

int main()
{
	int n, i, j, temp;

	cin >> n;

	vector<int> v(n);

	for (i = 0; i < n; i++) 
		cin >> v[i];

	/*Insertion  Sort Begin*/
	for (i = 1; i < n; i++)
	{
		temp = v[i];
		for (j = i - 1; j >= 0; j--)
		{
			if (v[j] > temp)
				v[j + 1] = v[j];
			else
				break;
		}

		v[j + 1] = temp;
	}
	/*Insertion Sort End*/

	for (int i = 0; i < n; i++)
		cout << v[i] << " ";
}

 

시간복잡도

1) 데이터가 이미 정렬된 케이스 : O(N)

버블 정렬, 선택 정렬과 다르게 삽입 정렬은 break 키워드가 존재한다. 

이미 정렬된 상태라면 정렬하려는 원소의 바로 앞 원소와 비교 시 break 키워드를 통해 즉시 for문을 탈출한다.

따라서 시간 복잡도는 외부 for문에 의해 결정되어 O(N)이다.

 

2) 데이터가 역순으로 정렬되어있는 케이스 : O(N^2)

역순으로 저장되어있는 데이터를 정렬하려면 매 사이클마다 첫 번째 원소까지 방문해서 데이터의 위치를 변경해야 한다.

비유가 적절할진 모르겠으나 버블 정렬처럼 작동한다고 생각하면 될 것 같다.

매 사이클마다 0번 원소에 접근하므로 1 + 2 + ... + (N-2) + (N-3) = N(N-1)/2 즉 O(N^2) 시간 복잡도를 가진다.

 

https://gmlwjd9405.github.io/2018/05/06/algorithm-insertion-sort.html