인트로
기초 정렬 알고리즘인 버블 정렬(Bubble Sort)과 시간 복잡도를 알아보자
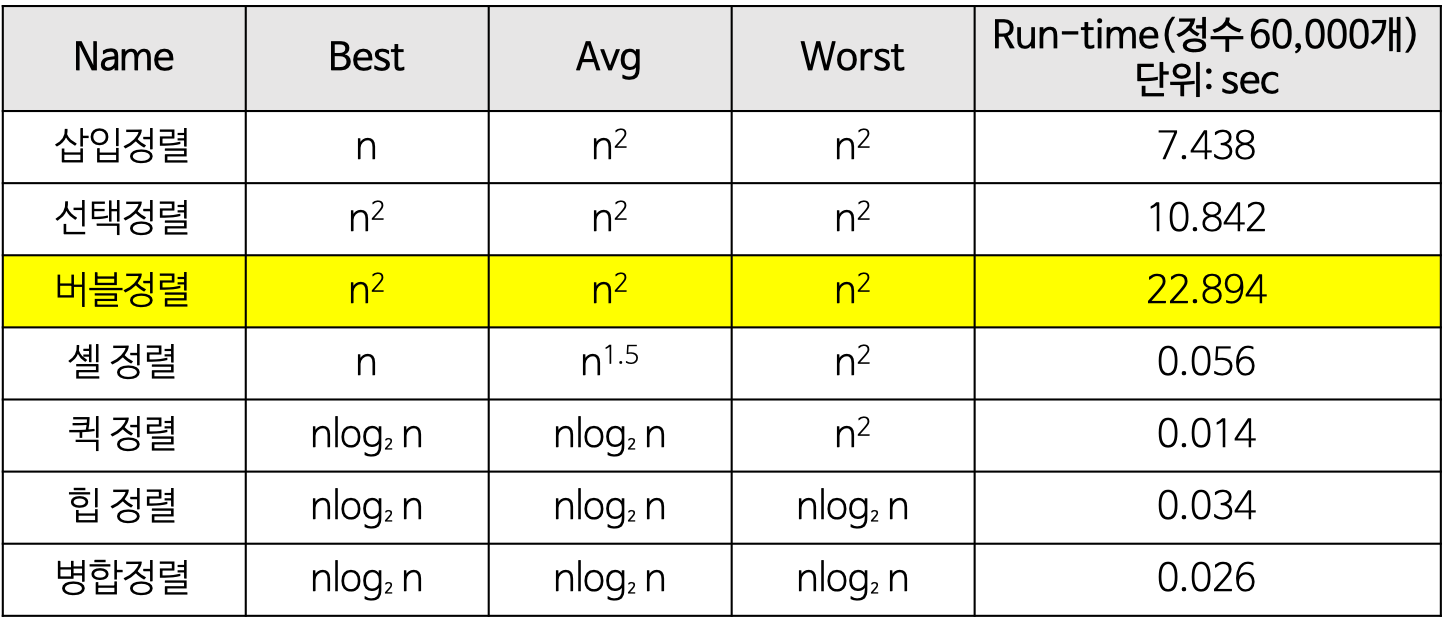
참고로 성능이 좋지 못해 버블 정렬이 사용될 일은 극히 드물다.
버블 정렬 활용 문제는 다음 포스팅을 참고하세요.
[Algorithm] level0 : Special Sort(구글 인터뷰)
[Algorithm] level0 : Special Sort(구글 인터뷰)
인트로 정렬을 알고리즘을 적용하는 문제이다. 어떤 정렬을 사용할진 문제를 읽어보고 고민하길 바란다. Special Sort(구글 인터뷰) 문제 N개의 정수가 입력되면 당신은 입력된 값을 정렬해야 한
kangworld.tistory.com
버블 정렬(Bubble Sort) : 개념
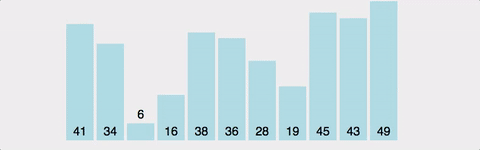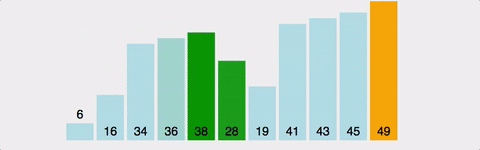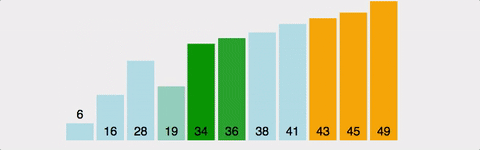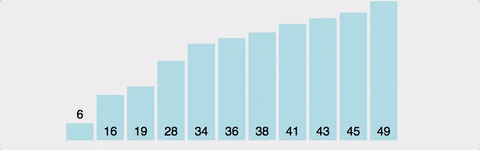
[ Cycle 1 ]
1. 배열의 "0"번 원소와 "1"번 원소를 비교해서 대소 여부에 따라 자리를 교체한다.
2. 배열의 "1"번 원소와 "2"번 원소를 비교해서 대소 여부에 따라 자리를 교체한다.
3. 이처럼 "N-2"번 원소와 "N-1"번(마지막) 원소를 비교하는 것으로 한 사이클이 끝난다.
4. 마지막 원소가 배열에서 가장 큰(작은) 숫자로 정렬되었다.
[ Cycle 2 ]
5. 다시 배열의 "0"번 원소와 "1"번 원소를 비교하고 대소 여부에 따른 자리 교체를 한다.
6. 배열의 인덱스를 1씩 증가하며 교체 작업을 반복한다.
7. [Cycle 1]에서 마지막 원소를 정렬했으므로 교체 작업을 "N-3"번 원소와 "N-2"번 원소를 마지막으로 한다.
버블 정렬(Bubble Sort) : 코드
#include <iostream>
#include <vector>
using namespace std;
int main()
{
int n;
cin >> n;
vector<int> v(n);
for (int i = 0; i < n; i++)
cin >> v[i];
/*Bubble Sort Begin*/
for (int i = 0; i < n - 1; i++)
{
for (int j = 0; j < n -i - 1; j++)
{
if (v[j] > v[j + 1])
{
int temp = v[j];
v[j] = v[j + 1];
v[j + 1] = temp;
}
}
}
/*Bubble Sort End*/
for (int i = 0; i < n; i++)
cout << v[i] << " ";
}시간복잡도
첫 번째 사이클 (i == 0)에서 비교 횟수 0 ~ (N - 2) : N-1회
두 번째 사이클 (i == 1)에서 비교 횟수 0 ~ (N - 3) : N-2회
.
.
.
마지막 회전(i == N-2)에서 비교 횟수 : 1회
(N-1) + (N-2) + (N-3)... + 1 = N(N-1)/2
즉 시간 복잡도는 O(N^2)이다.
(+ 선택 정렬과 투톱으로 효율이 안 좋으며 쉬운 정렬)
'Algorithm > 정렬' 카테고리의 다른 글
| [Algorithm] 병합 정렬(Merge Sort) 코드와 시간 복잡도 (0) | 2021.10.10 |
|---|---|
| [Algorithm] 두 배열을 정렬하며 합치기 : 병합 정렬 기초 (0) | 2021.10.09 |
| [Algorithm] 삽입 정렬(Insertion Sort) 코드와 시간 복잡도 (+ 예제) (0) | 2021.08.20 |
| [Algorithm] 선택 정렬(Selection Sort) 코드와 시간 복잡도 (0) | 2021.08.18 |

