
인트로
본 포스팅에선 조합을 구하는 코드를 소개하려 한다. 결론부터 말하면 재귀 함수(DFS)로 조합을 구할 수 있다.
조합이란 n개 중에 r개를 "순서에 무관하게" 뽑는 경우의 수로 다음과 같이 표현한다. $_nC_r=\frac{n!}{(n-r)!r!}$
이와 유사하게 순서를 고려해 n개 중에 r개를 뽑는 것을 순열이라고 한다.
※참고 - 순열 포스팅
[Algorithm] 순열(Permutation) 구현 코드
조합 : 코드
순서에 무관하게 숫자를 뽑기때문에 별도의 visited 배열이 필요하지 않다.
#include <iostream>
using namespace std;
int arr[10] = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 };
int cnt, n, r;
int order[4];
void combination(int now, int pos)
{
if (now == r)
{
for (int i = 0; i < r; i++)
{
cout << arr[order[i]] << " ";
}
cout << endl;
cnt++;
return;
}
for (int idx = pos; idx < n; idx++)
{
order[now] = idx;
combination(now + 1, idx + 1);
}
}
int main()
{
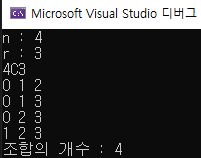
cout << "n : ";
cin >> n;
cout << "r : ";
cin >> r;
cout << n << 'C' << r << endl;
combination(0, 0);
cout << "조합의 개수 : " << cnt;
}
'Algorithm > 탐색' 카테고리의 다른 글
| [Algorithm] 다익스트라 알고리즘 : 음수 간선이 있으면 안 되는 이유 (2) | 2021.10.12 |
|---|---|
| [Algorithm] 유니온 파인드 (Union-Find) : Disjoint-set 표현 (0) | 2021.10.06 |
| [Algorithm] 순열(Permutation) 구현 코드 (0) | 2021.10.04 |
| [Algorithm] 이진 탐색 (이분 탐색, Binary Search) 코드와 시간 복잡도 (0) | 2021.09.16 |
| [Algorithm] A* 알고리즘 : 최단 경로 탐색 (4) | 2021.09.03 |

