
소수 찾기 알고리즘도 약수 찾기와 비슷한 문제로 많이 소개된다.
코딩을 입문하거나 알고리즘을 공부하는 사람들이 한 번쯤 거쳐가는 문제라고 생각한다.
본 포스팅에선 임의의 숫자가 입력되고 소수인지 판별하는 문제가 아닌! 구간 내에 소수가 몇 개 존재하는지 출력하는 문제를 소개하려 한다.
+ 본 문제의 출저 https://programmers.co.kr/learn/courses/30/lessons/12921
코딩테스트 연습 - 소수 찾기
1부터 입력받은 숫자 n 사이에 있는 소수의 개수를 반환하는 함수, solution을 만들어 보세요. 소수는 1과 자기 자신으로만 나누어지는 수를 의미합니다. (1은 소수가 아닙니다.) 제한 조건 n은 2이상
programmers.co.kr
문제
1부터 입력받은 숫자 n 사이에 있는 소수의 개수를 반환하는 함수, solution을 만들어 보세요.
소수는 1과 자기 자신으로만 나누어지는 수를 의미합니다. (1은 소수가 아닙니다.)
※제한 조건
n은 2이상 1000000이하의 자연수입니다.
입력
10
출력
4
입출력 설명
입출력 예
1부터 10 사이의 소수는 [2,3,5,7] 4개가 존재하므로 4를 반환
코드 설명
지금 소개할 코드는 가장 쉽게 생각할 수 있는 코드다.
이중 for문 2부터 n까지 돌며 소수인지 체크하고 소수라면(isPrime == true) answer를 증가시킨다.
문제는 i가 n에 가까워질수록 내부 for문도 n회에 가깝게 반복하게 되므로 시간 복잡도는 O(N^2)이다.
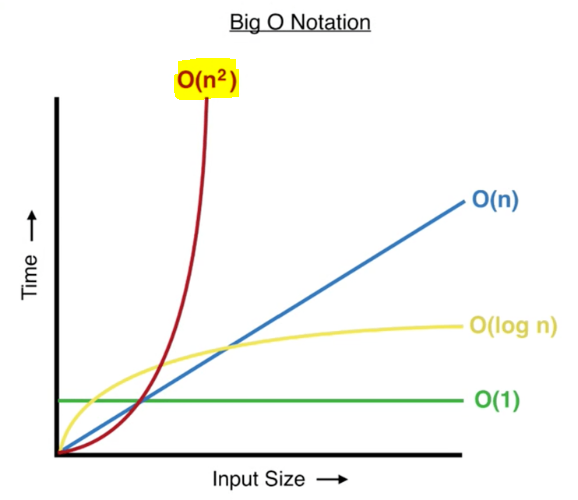
O(N^2)의 시간복잡도를 가지게 되면 input의 값이 커질수록 시간은 기하급수적으로 올라간다.
실행 결과를 보면 시간 초과가 발생한 것을 확인할 수 있다.
#include <string>
#include <vector>
using namespace std;
int solution(int n) {
int answer = 0;
bool isPrime;
for(int i = 2; i <= n; i++)
{
isPrime = true;
for(int j = 2; j < i; j++)
{
if(i % j == 0)
{
isPrime = false;
break;
}
}
if(isPrime)
answer++;
}
return answer;
}
코드 설명전에 에라토스테네스의 체에 대해서 알아보고 넘어가자.
에라토스테네스 아저씨 이름이 어려워서 개념도 어려워 보이지만 알아보면 별거 아니다.
굉장히 수학적으로 소수를 찾는 방법인데 그림을 보며 이해하자.
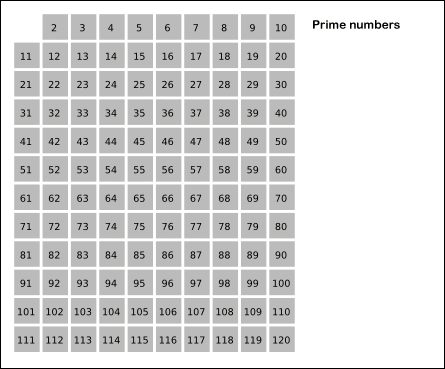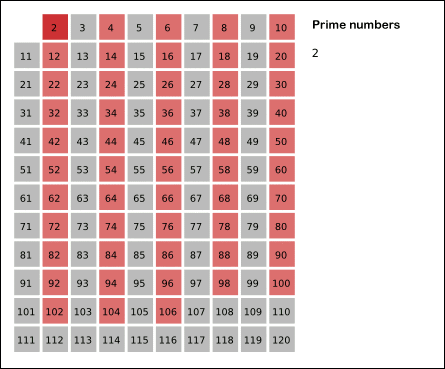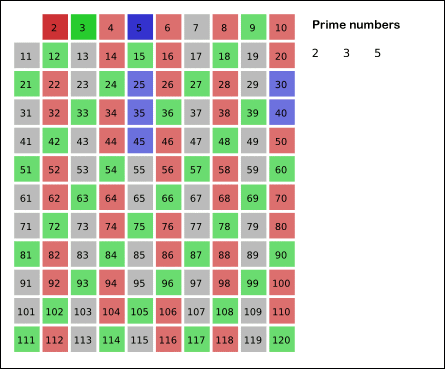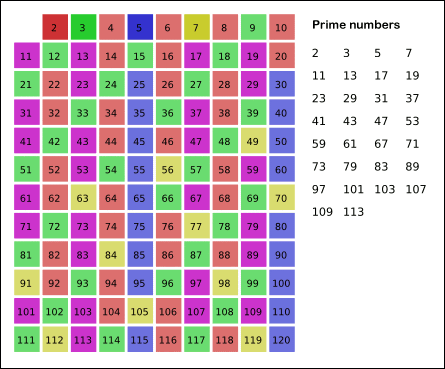
그림에서 N을 120까지로 제한했으니 N이 120이라 가정하자.
[1] 2는 소수이다.
[2] 2를 제외한 2의 배수들은 소수가 아니다. 2를 약수로 갖고 있으니. 따라서 2의 배수들을 소수가 아니라고 체크한다.
[3] 3은 소수이다.
[4] 3을 제외한 3의 배수들은 소수가 아니다.
[5] 4는 소수가 아니므로 넘어간다.
[6] 5는 소수이다.
... 120까지 반복하면 색칠하지 않은 소수들만 남게 된다.
코드 설명
bool형 벡터를 선언하고 true로 초기화 시킨다.
반복문을 돌며 벡터의 인덱스와 동일시되는 숫자가 소수임을 true 혹은 false로 벡터에 저장한다.
[1] 2는 소수인가? v[2] == true 만족
[2] 2의 배수들을 false로 저장
[3] answer 증가
[4] 3은 소수인가? v[3] == true 만족
[5] 3의 배수들을 false로 저장
[6] answer 증가
[7] 4는 소수인가? v[4] == true 불만족
[8] 5는 소수인가?...
이 과정을 120까지 반복한다.
#include <string>
#include <vector>
using namespace std;
int solution(int n) {
int answer = 0;
vector<bool> v(n+1, true);
for(int i = 2; i <= n; i++)
{
if(v[i] == true)
{
for(int j = 2; j*i <= n; j++)
{
v[j*i] = false;
}
answer++;
}
}
return answer;
}
에라토스테네스의 체를 사용하면 시간 복잡도가 O(Nlog(logN))으로 O(N)에 가깝다고 한다.
'Algorithm > 프로그래머스 : Level 1' 카테고리의 다른 글
| [프로그래머스 Level 1] 내적 (0) | 2021.10.17 |
|---|---|
| [프로그래머스 Level 1] 키패드 누르기 (2020 카카오 기출) (0) | 2021.10.17 |
| [프로그래머스 Level 1] 숫자 문자열과 영단어 (2021 카카오 기출) (0) | 2021.10.17 |
| [프로그래머스 Level 1] 신규 아이디 추천 (2021 카카오 기출) (0) | 2021.10.17 |
| [프로그래머스 Level 1] 로또의 최고 순위와 최저 순위 (0) | 2021.10.17 |

