
🖊️ 문제
양의 정수 x에 대한 함수 f(x)를 다음과 같이 정의합니다.
- x보다 크고 x와 비트가 1~2개 다른 수들 중에서 제일 작은 수
예를 들어,
- f(2) = 3 입니다. 다음 표와 같이 2보다 큰 수들 중에서 비트가 다른 지점이 2개 이하이면서 제일 작은 수가 3이기 때문입니다.
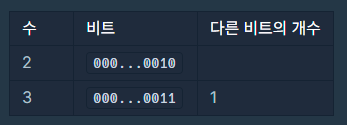
- f(7) = 11 입니다. 다음 표와 같이 7보다 큰 수들 중에서 비트가 다른 지점이 2개 이하이면서 제일 작은 수가 11이기 때문입니다.

정수들이 담긴 배열 numbers가 매개변수로 주어집니다. numbers의 모든 수들에 대하여 각 수의 f 값을 배열에 차례대로 담아 return 하도록 solution 함수를 완성해주세요.
제한사항
- 1 ≤ numbers의 길이 ≤ 100,000
- 0 ≤ numbers의 모든 수 ≤ 1015

🖥️ 코드
#include <string>
#include <vector>
using namespace std;
vector<long long> solution(vector<long long> numbers)
{
vector<long long> answer;
for (int i = 0; i < numbers.size(); i++)
{
if (numbers[i] & 1)
{
for (int j = 0; j < 64; j++)
if (!(numbers[i] & ((long long)1 << j)))
{
answer.push_back(numbers[i] + ((long long)1 << (j - 1)));
break;
}
}
else answer.push_back(numbers[i] + 1);
}
return answer;
}
🤔 나의 생각
- 본 문제로 비트 연산에 조금 눈이 트였다.
- 일단 문제 자체는 굉장히 재밌었다. 문제 해결을 위해 두 가지 경우를 생각해야 하는데 x가 짝수일 때, x가 홀수일 때.
- x가 짝수일 때, 가장 오른쪽 비트를 1로 바꿔주면 x보단 크면서 가장 작은 수가 된다. (매우 직관적임)
- x가 홀수일 때, 오른쪽부터 왼쪽으로 비트를 탐색했을 때 패턴 01을 만나면 10으로 바꿔줘야 한다. ( 0111 -> 1011)
- 일단 x보단 커야 하므로 가장 처음 만난 0을 1로 바꿔주는 건 당연한 일이다. 그런데 만약 여기서 멈춘다면 x보단 크고 비트 하나를 바꿨을 때 기준으로 가장 작은 수다.
- 우린 비트 두 개를 바꿨을 때 가장 작은 수를 원하므로 0은 x보다 크다는 조건을 만족하기 위해 1로 바꿔주고 큰 수중 가장 작은 수를 만족하기 위해 뒷자리 비트를 0으로 바꿔주는 것이다.
- 상수에 32비트를 넘어가는 shift 연산을 하려면 앞에 (long long)을 붙여서 64비트 데이터형으로 처리해야 한다.
'Algorithm > 프로그래머스 : Level 2' 카테고리의 다른 글
| [프로그래머스 Level 2] 영어 끝말잇기 (0) | 2021.11.22 |
|---|---|
| [프로그래머스 Level 2] 삼각 달팽이 (0) | 2021.11.21 |
| [프로그래머스 Level 2] 프렌즈4블록 (2018 카카오 기출) (0) | 2021.11.21 |
| [프로그래머스 Level 2] 피로도 (0) | 2021.11.21 |
| [프로그래머스 Level 2] H-Index (0) | 2021.11.19 |

